We consider a firing rate neural network model used to describe disinhibited cortical tissue, whereby an excitatory population of cells u undergoes spike-frequency adaptation (Pinto & Ermentrout, 2001)

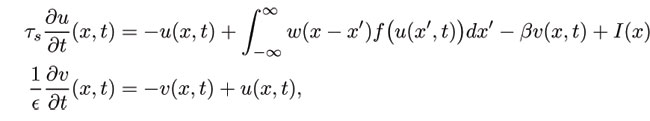
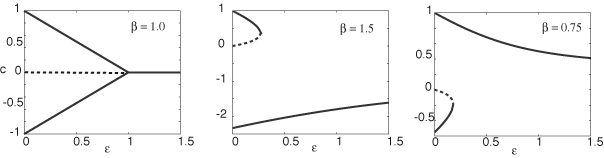
Traveling front solutions for I = 0 exist when the effect of adaptation is weak (small β ), the profile of which is a shrunken version of the front in the scalar system (β = 0 ). For smooth firing rate functions f, we subsequently carry out a perturbation expansion in powers of the wavespeed c to show that a stationary front can undergo a supercritical pitchfork bifurcation at a critical rate of negative feedback, leading to bidirectional front propagation. In the case of a spatially homogeneous input, the fronts bifurcate according to a codimension 2 cusp bifurcation.

Analogous to the case of reaction diffusion systems, the front bifurcation acts as an organizing center for a variety of nontrivial dynamics including the formation of oscillatory fronts or breathers. We show how the latter can occur through a Hopf bifurcation from a stationary front in the presence of a weak stationary input inhomogeneity.

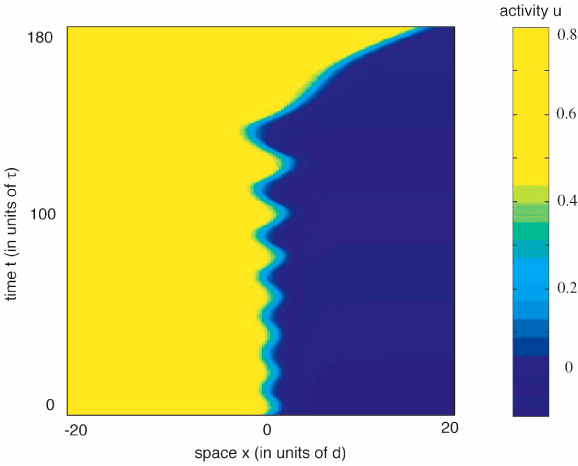
The existence and stability of stationary fronts is pursued in an exactly solvable model, which is obtained by taking the high gain limit of the sigmoid function f such that f(u) = H (u- κ) where H is the Heaviside function and κ a threshold. The exactly solvable model allows the study of oscillatory fronts beyond the weak input regime. Rather than perturbing about the homogeneous case, we are able to consider a large input amplitude for which wave propagation failure occurs due to the pinning of a stationary front. A subsequent reduction in the amplitude of the input then induces a Hopf instability leading to the formation of a breather. The amplitude of osciallations grow as the input is further decreased beyond the bifurcation. A movie of a breathing front is located here.

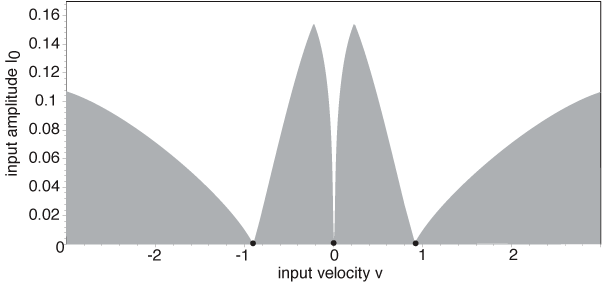
In the exactly solvable model, we also derive conditions for the locking of a traveling front to a moving input I(x, t) = Io X(x-ct), and show how locking depends on both the amplitude and speed of the input. The idea of locking to a moving input is explored more deeply within the context of stimulus-locked pulses. In the image below the region of locking is denoted by white. As Io --> 0 the tongues approach the 3 natural waves supported by the network in the absence of an input.

The existence and stability of stationary pulse solutions which are induced by a Gaussian-like input. In order to construct exact wave solutions, we consider the firing rate model (Pinto & Ermentrout, 2001) with the inclusion of a stationary input I(x)

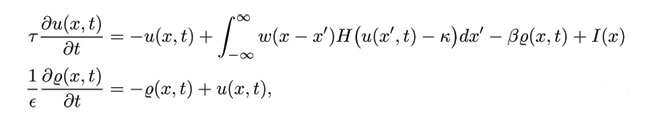
In the absence of an input, a stationary pulse solution, if it exists, is unstable, acting as a separatrix that either generates a pair of counter-propagating pulses or a return to the resting state. However, a stationary pulse is stabilized by a sufficiently large input, leading to wave propagation failure of an approaching wave. The stable pulse disappears in one of two ways, (i) for (ε>β) a stable-unstable pair of stationary pulses simply annihilate in a saddle-node bifurcation, and (ii) for (ε<β), the stable pulse loses stability in a Hopf bifurcation. Although there are multiple bifurcation senarios, the following illustrates the general idea. Stationary pulses exist for all input strengths above the saddle-node point and are stable for sufficiently large inputs.

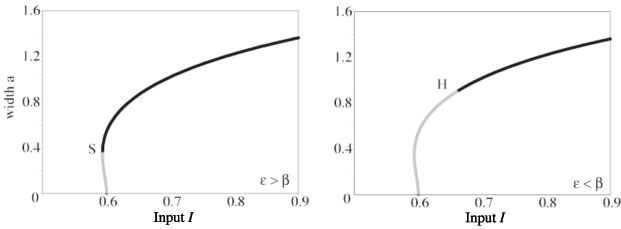
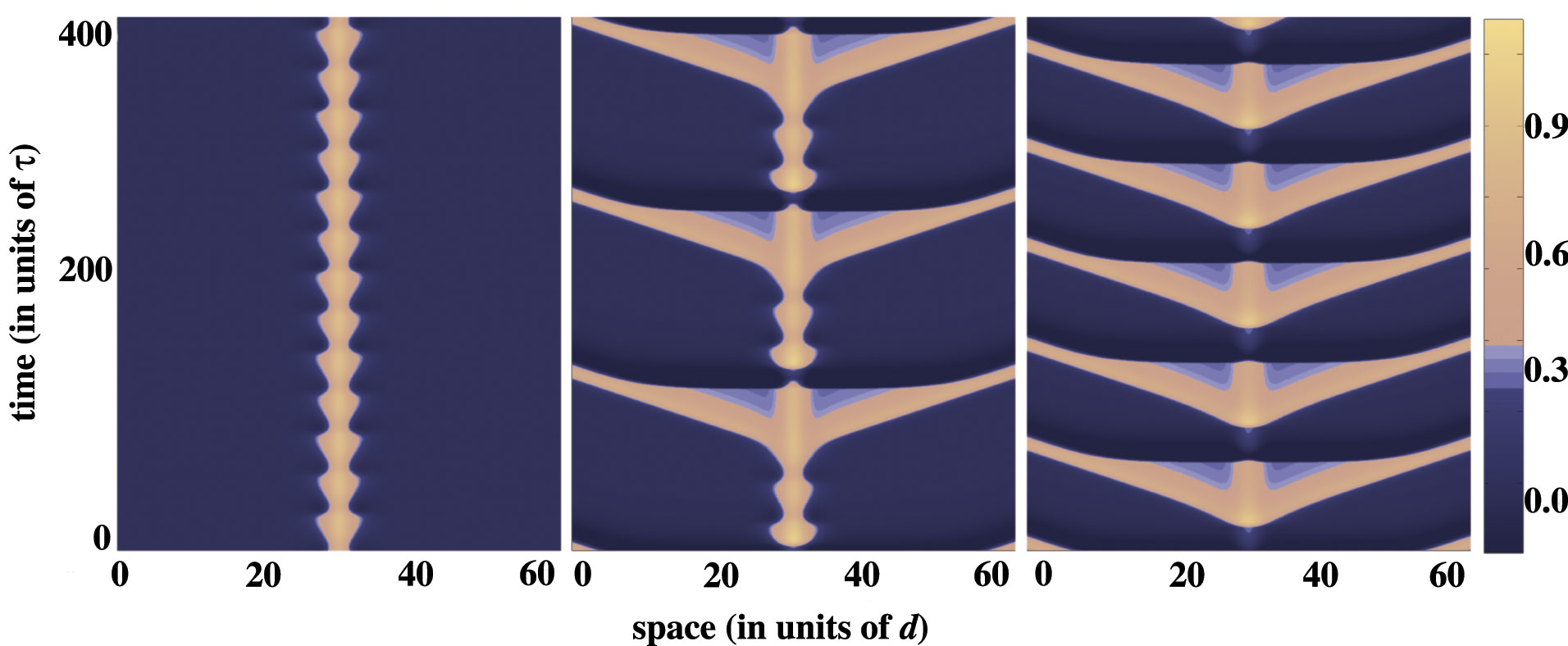
A supercritical or subcritical Hopf bifurcation occurs at some value of input strength above the saddle-node point, leading either to a periodic modulation of the stationary pulse or breather, in the supercritical case, or to a subthreshold bump, in the subcritical case. The breather subsequently undergoes a secondary instability leading to a pulse-emitter, a breather-like solution that periodically emits traveling pulses into the surrounding medium. Movies of the breathers and emitters are generated by numerical simulation. Interestingly the breather may lose stability due to a subcritical period-doubling bifurcation. The evidence for this is that a more extensive cascade of supercritical period-doubling bifurcations occurs for increasingly large input widths, followed by a sharp transition to the pulse-emitter, shown in the following space-time plots and phase curves. In the case of the phase curves, only one spatial point is displayed, however, all spatial points are qualitatively similar.

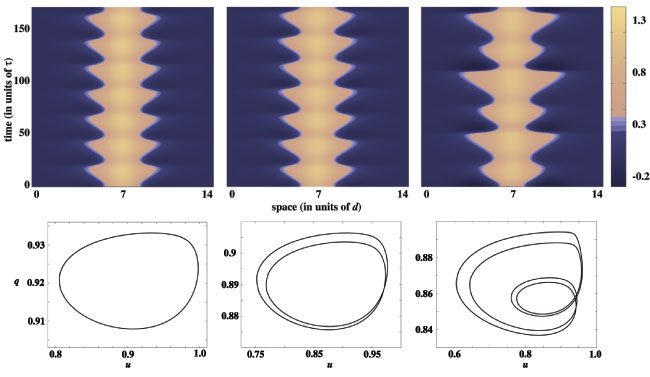
In the following plot, the input width is such that a supercritical period-doubling does not occur. In the left column the resulting emitter is shown beyond the bifurcation, while the right column presents the phase portraits of both the limit cycle before bifurcation (black) and the more complicated limit cycle of the emitter after the bifurcation (gray). The new orbit appears to be weaving its way through the unstable limit cycle, before making the large excursion corresponding to wave emission.

Moreover, for a range of inputs after the transition to the emitter, there is mode--locking between the oscillation frequency of the breathings and the rate of wave emission, giving way ultimately to regular emission.

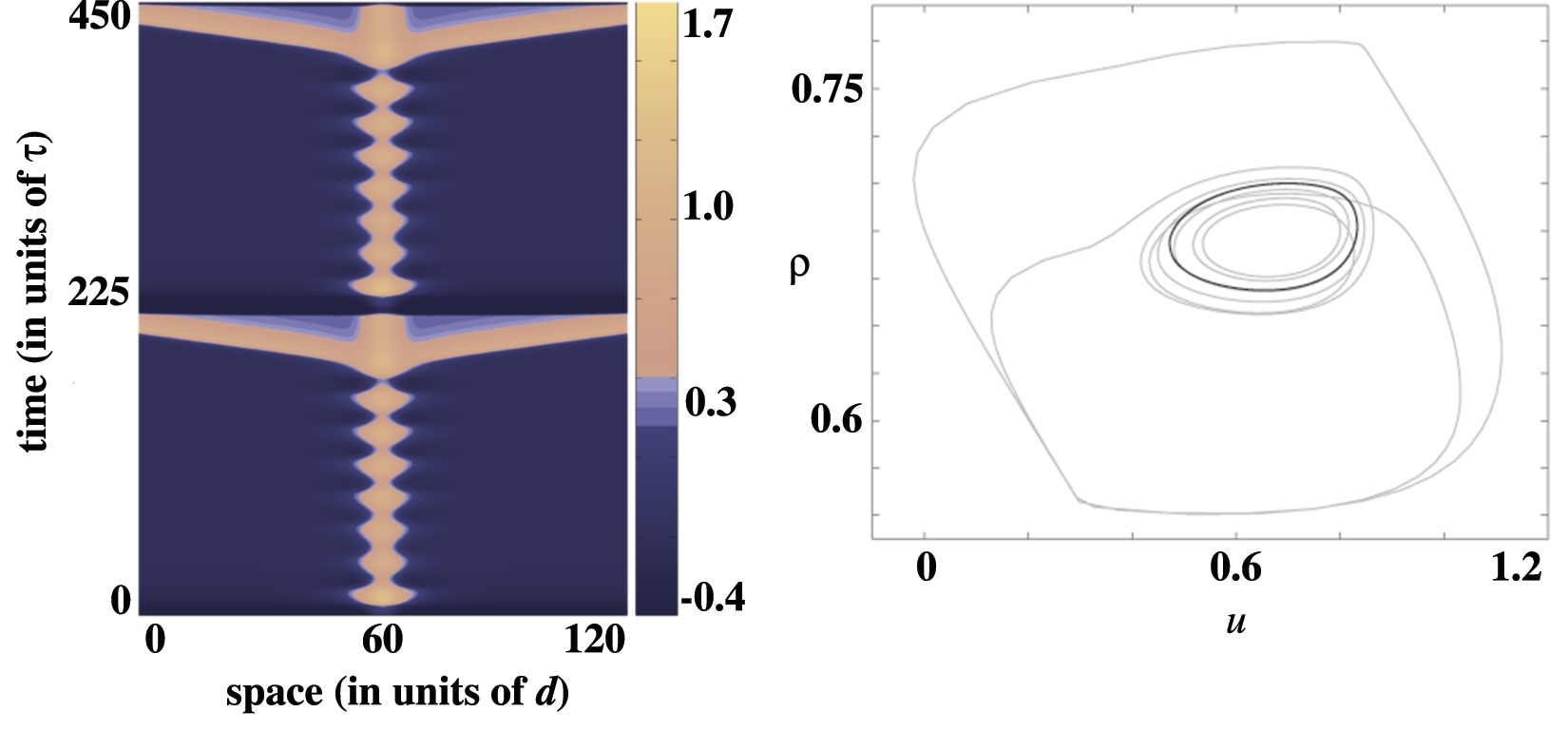
The pulse-emitter eventually disappears for sufficiently small inputs, and the medium approaches a subthreshold bump, i.e., the rest state. Interestingly, the breather and pulse-emitter can persist at inputs below the saddle-node point, i.e., below the minimum input necessary for the existence of a stationary pulse. Finally, analogous forms of oscillatory waves are also shown to occur in a more biophysically realistic conductance--based model that features a slow potassium current to induce spike-rate adaptation, lending further support for the ability of firing rate models to describe the activity of detailed biophysical models.

Movies of the breathers are located here.

We extend our analysis to radially symmetric pulses in a two–dimensional network in which the weight function w is either excitatory (positive) or Mexican hat.

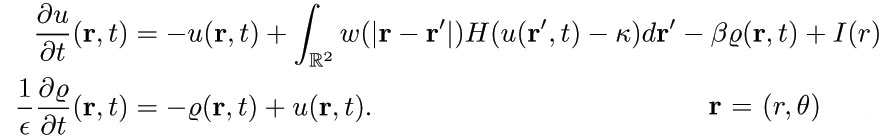
The Mexican hat weight, in this case, arises from the excitatory-inhibitory model with particular assumptions on the firing rates, subject to the additional assumptions that the excitatory population exhibits adaptation and the fast inhibitory population operates in quasi-steady-state.

Many of the results from the one-dimensional excitatory case carry over, including radially-symmetric breathing pulses:

When the Hopf bifurcation is supercritical (as determined via numerical simulations), well beyond the bifurcation point, the breather can transition to a wave emitter that gives rise to outward propagaing circular waves when such waves supported by the medium:

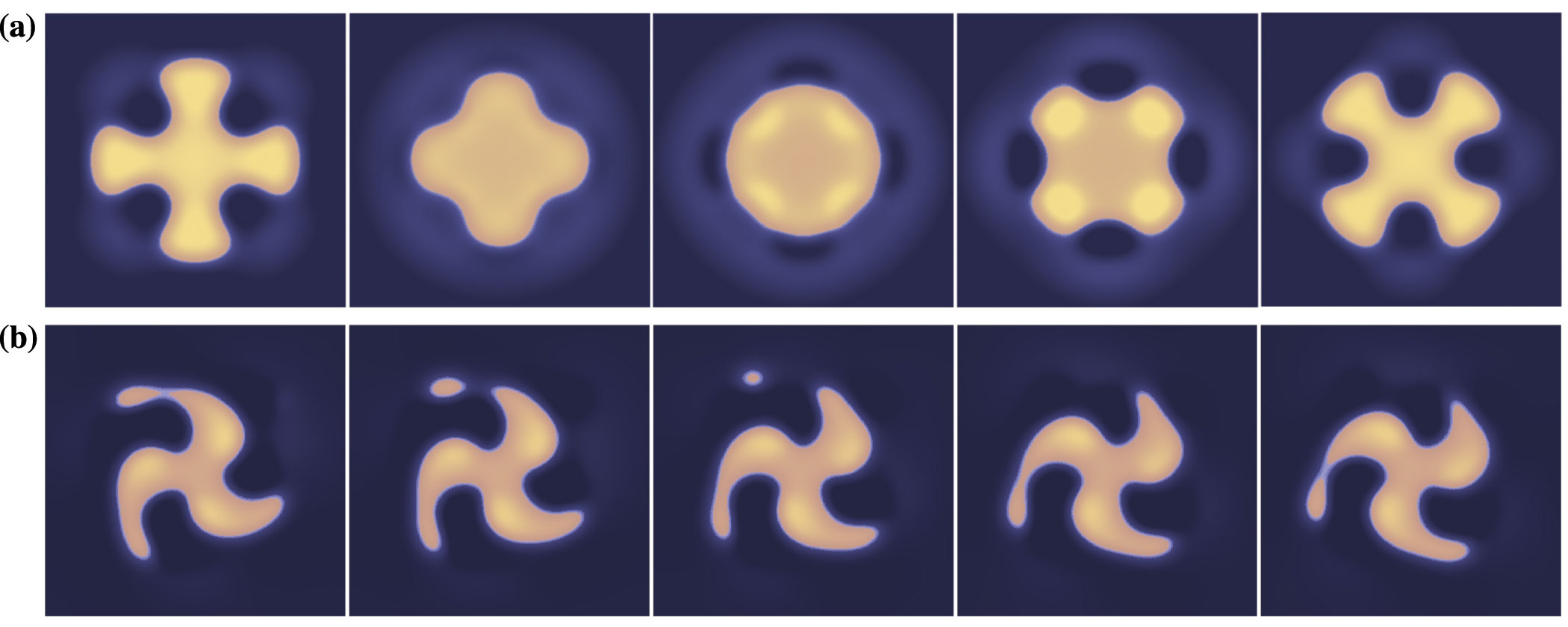
Interestingly, the Mexican hat weight function is capable of producing nonradially symmetric breathers, the number of lobes of which is consistent with the dominant unstable Fourier mode associated with perturbations of the pulse boundary. Furthermore, other spatially-localized solutions seem to coexist, including spatially-localized rotating solutions, or rotors. Movies of the 2D breathers and rotors are included here. The difference in the effect of the different weight functions is exemplified by the fact that, depending on the strength and width of the input, higher order spatial modes associated with the linearization may dominate the instability, whereas in the excitatory case the lowest order, radially symmetric mode always dominates. Furthermore, we expect the full three variable model to have qualitatively similar results to the quasi-steady-state approximation.

Simulations were done on a rectangular grid and an irregular polar grid which maintains equal contribution of each grid point (area surrounding) to the integral. Interestingly, the primary difference in the effect of the rectangular grid is that modes which are commensurate with the grid, e.g. n=4, often give rise to strictly expanding/contracting breathers as shown below (a).

(b) Beyond the bifurcation point the activity can develop long and narrow lobes, sometimes emitting transient pulses of activity. In general the inclusion of inhibition in this kind of network tends to occlude traveling waves. However, if the threshold κ is reduced to very small but nonzero values, e.g. 0.01, nonradially symmetric emitters may also be found.

Finally we consider the effect of a Gaussian-like input moving with constant speed v, in which case we have

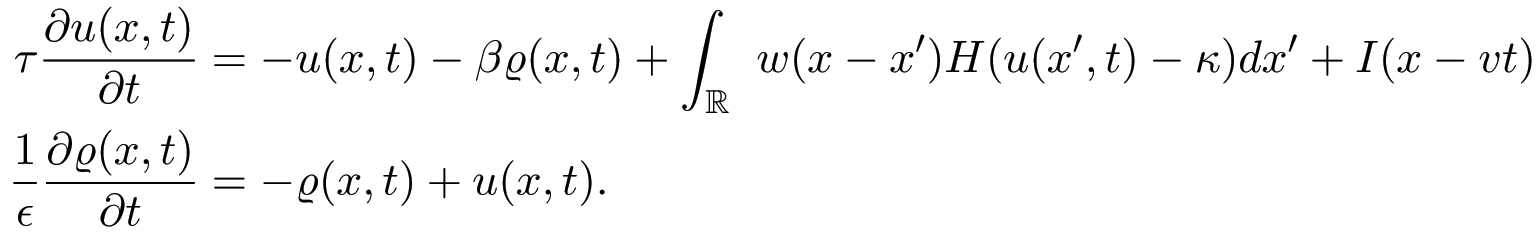
Working in the moving frame of the input, we use the input strength Io and speed v as bifurcation parameters, to determine the existence and stability of stimulus-locked pulses, and construct existence tongues in the (v, Io)-plane, whose tips at Io = 0 correspond to the intrinsic waves of the homogeneous network. In the case of an exponential weight distribution, we find that there are two tongues in the positive v domain, corresponding to an unstable/stable pair of right-moving intrinsic (I = 0) waves.

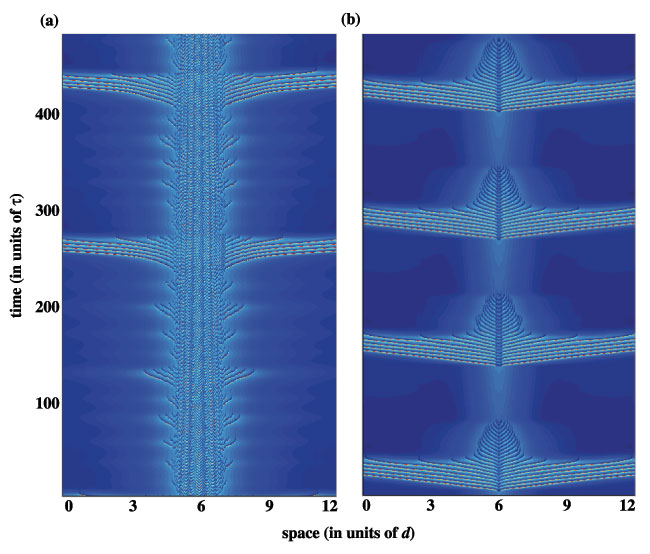
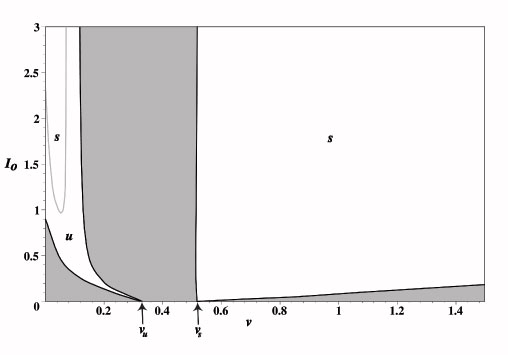
We determine the stability of the waves within these existence tongues by first constructing the Evans function and then numerically calculating its zeros. In the figure, white denotes the tongue, s (u) denotes stability (instability) of the pulse. We show that, as the input is reduced, a stimulus-locked wave within the tongue of the unstable intrinsic wave can undergo a Hopf bifurcation (gray curve) leading to the emergence of a traveling oscillatory wave. The latter takes the form of either a breather or a pulse-emitter in the moving frame of the stimulus, depending upon the direction of bifurcation. In the limit v --> 0 our results reduce to those obtained for stationary inputs. Numerical simulations illustrate the formation of traveling breathers and pulse-emitters.

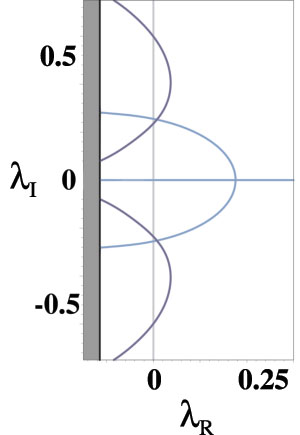
Simulations suggest that the left branch of the Hopf curve (gray) corresponds to a supercritical bifurcation, while the right branch is subcritical without a sharp transition to a breathing pulse. Crossing the "subcritical" branch of the Hopf curve, we find a region of activity moving with the input whose right boundary oscillates with increasing amplitude. After a critical point, the system emits a natural traveling pulse, whose speed is faster than that of the input, as shown in the following figure. On the right is a graph of the zero-sets of the real (dark blue) and imaginary (light blue) parts of the Evans function, the intersections of which identify eigenvalues.

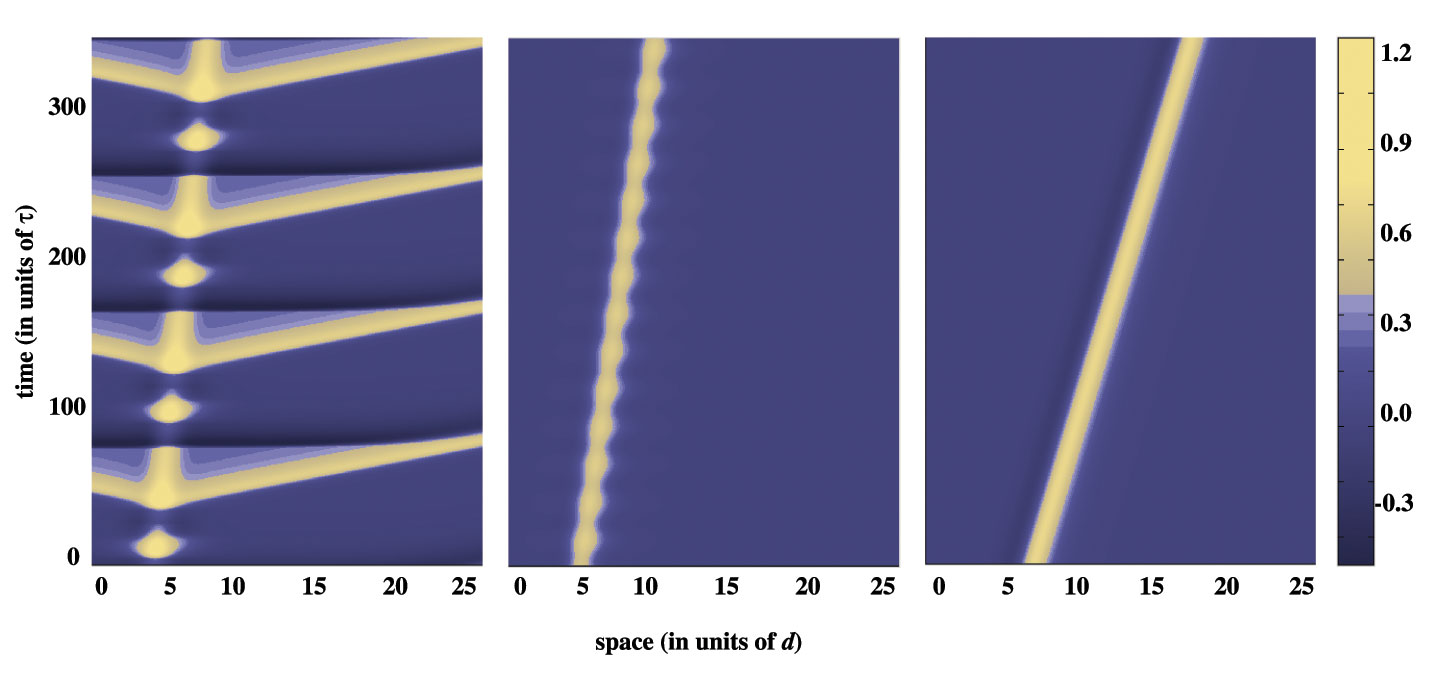
When the left-hand supercritical branch of the Hopf curve is crossed by reducing Io or v, we find a smooth transition to a stimulus-locked traveling breather. The breathing solutions continue to persist in a subregion of the (v, Io)-plane bounded to the right by the left (supercritical) branch of the Hopf curve. As one moves in this subregion away from the left Hopf branch, the amplitude of the oscillations grows. After some point, the breathing solution disappears and a new type of temporally periodic solution appears, each cycle of which is characterized by one or more breathing pulse oscillations followed by the emission of a pair of natural waves, possibly intermixed with interludes of subthreshold behavior. This transition from stimulus-locked pulse to breather to emitter is illustrated in the following figure.

The transition from breathing pulse to emitting pulse may be due to a subcritical period-doubling bifurcation, a possible candidate for the transition to pulse-emitter described in the case of the stationary input above. This type of pulse-emitting solution appears to be part of a family of related responses of the system to a localized input, occuring whenever the associated traveling pulse (or breather) is either unstable or nonexistent. This includes the emitters found within the region between the subcritical Hopf curve and the stable right tongue and, consequently, there is a smooth transition of behaviors joining the two regions, as shown in the following figure.

Analogous to the case of a stationary input, more complicated mode-locking phenomena is also observed and can be seen in a movie.