Spatially–Localized Synchronous Oscillations in the E-I Map: 1:2 Resonance Bifurcation |
1:2 Resonance Bifurcation | |||||
| The following movies are sequences of phase portraits for the E-I map in the vicinity of the codimension 2 point for a strong resonance bifurcation. In this case, the bifurcation occurs on a period 2 orbit (typically a fixed point).
E-I map —
a 2–D implicit discrete map describing spatially–localized synchronous oscillations exhibited
in a network of neuronal conductance-based models extended along one spatial dimension.
The network is composed of an excitatory–inhibitory pair of neuronal populations that are mutually coupled through distance–dependent synaptic coupling where:
For details see the relevant publication:
S. E. FOLIAS & G. B. ERMENTROUT,
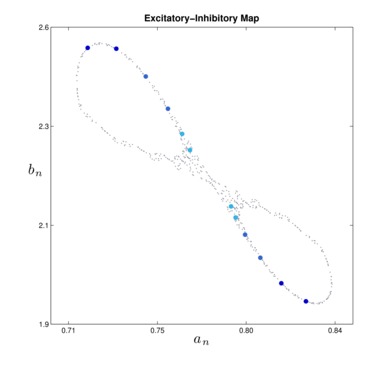
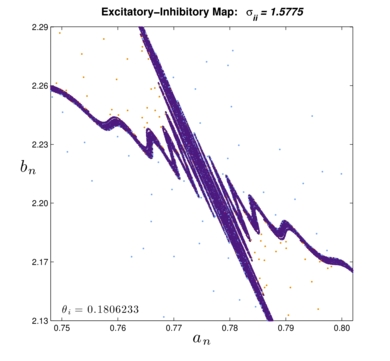
Spatially–localized synchronous oscillations in 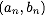 – phase plane for decreasing θi and fixed σii. Each orbit contains up to 100,000 iterates and is colored with two colors distinguishing transient from long–term behavior: – phase plane for decreasing θi and fixed σii. Each orbit contains up to 100,000 iterates and is colored with two colors distinguishing transient from long–term behavior:
The light blue transient leads to dark purple long–term behavior
The yellow-orange transient leads to red long–term behavior. If both purple and red overlap, then only purple is shown. · Most movies are mpeg–4 part 2 (mpeg–4 improved) unless indicated otherwise Instructions for viewing
· Mouse–over an image (i.e., place cursor over image) to animate a sequence of snapshots for the movie.
· Click a link next to FORMATS to download the movie. | |||||
Special Edition Movie (new!) | |||||
|
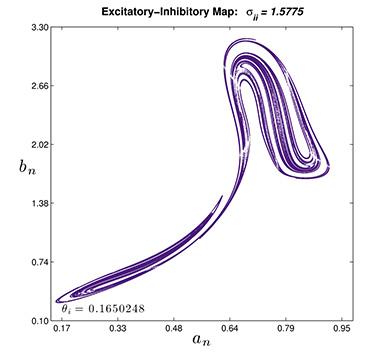
 SIZE: 609 MB PHASE PORTRAITS: 8200 FORMATS: .mp4 (mpeg4) CONTENT: An equilibrium undergoes a flip bifurcation to a stable period 2 orbit which subsequently undergoes a 1:2 strong resonance bifurcation exhibiting a flip bifurcation, Neimark–Sacker bifurcation, weak resonances and chaos, a homoclinic bifurcation with a pair of double homoclinic tangles, and the analogue of a saddle–node bifurcation of limit cycles that causes orbits to diverge. The movie ends with an evolution of the seahorse attractor. |
||||
Short Movies | |||||

|
 SIZE: 24 MB PHASE PORTRAITS: 447 FORMATS: .mp4 (mpeg4) CONTENT: A close–up near the homoclinic bifurcation corresponding to the longer movie for σii=1.58 above. |
||||
|
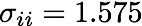 SIZE: 8 MB PHASE PORTRAITS: 1 FORMATS: .mp4 (mpeg4) CONTENT: Animation of a single trajectory when the double homoclinic tangle is present to demonstrate how the phase portrait is generated. A set of consecutive iterates is colored blue with darker blues indicated more advanced iterates. The set of iterates is then advanced leaving behind gray dots that denote previous iterates. |
||||
High Resolution Movies | |||||

|
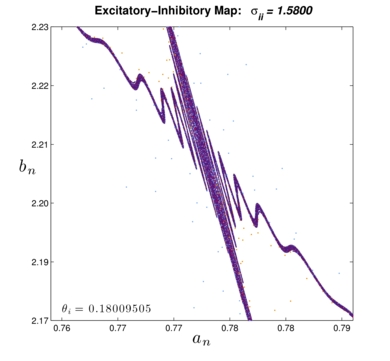
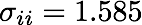 SIZE: 20 MB PHASE PORTRAITS: 1000 FORMATS: .mp4 (mpeg4) CONTENT: Beginning well after the Neimark–Sacker bifurcation, the movie exhibits a partial sequence of the bifurcations, including weak resonances and chaos and the homoclinic bifurcation that leads to a large stable closed curve exhibiting resonances. |
||||
|
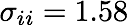 SIZE: 57 MB PHASE PORTRAITS: 2000 FORMATS: .mp4 (mpeg4) CONTENT: Beginning well after the Neimark–Sacker bifurcation, the movie exhibits a partial sequence of the bifurcations, including weak resonances and chaos and the homoclinic bifurcation that leads to a large stable closed curve exhibiting resonances. |
||||
|
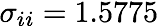 SIZE: 117 MB PHASE PORTRAITS: 2850 FORMATS: .mov | .mp4 (H.264) CONTENT: An equilibrium undergoes a flip bifurcation to a stable period 2 orbit which subsequently undergoes a 1:2 strong resonance bifurcation exhibiting a flip bifurcation, Neimark–Sacker bifurcation, weak resonances and chaos, a homoclinic bifurcation with a pair of double homoclinic tangles, and the analogue of a saddle–node bifurcation of limit cycles that causes orbits to diverge. |
||||

|
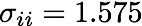 SIZE: 292 MB (154 MB H.264) PHASE PORTRAITS: 3977 FORMATS: .mp4 (mpeg4) | .mp4 (H.264) CONTENT: Beginning well after the Neimark–Sacker bifurcation, the movie exhibits a partial sequence of the bifurcations, including weak resonances and chaos and the homoclinic bifurcation that leads to intricate dynamics before orbits start to diverge. |
||||
Medium Resolution Movies | |||||

|
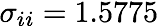 SIZE: 71 MB PHASE PORTRAITS: 2850 FORMATS: .mov | .mp4 (H.264) CONTENT: An equilibrium undergoes a flip bifurcation to a stable period 2 orbit which subsequently undergoes a 1:2 strong resonance bifurcation exhibiting a flip bifurcation, Neimark–Sacker bifurcation, weak resonances and chaos, a homoclinic bifurcation with a pair of double homoclinic tangles, and the analogue of a saddle–node bifurcation of limit cycles that causes orbits to diverge. |
||||
Stefanos E. Folias
10.10.2010
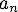 —
— 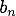 —
—