Rolle's Theorem

The Mean Value Theorem is a useful tool that generalizes Rolle's Theorem. Draw a line from the starting point on the graph to the ending point. This line is horizontal. Rolle's theorem said that somewhere in between there was a horizontal tangent line.

Mean Value Theorem: If f(x) is
1). continuous on [a,b] and
2). f(x) is differentiable on (a,b) and
there is some number c in (a,b) such that f'(c)=[f(b)-f(a)]/(b-a).

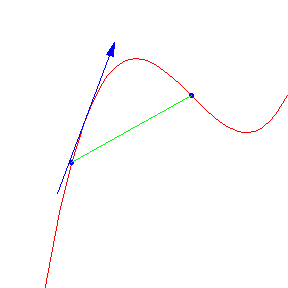
Consider the graph of the function below. The green line is drawn from the starting point to the ending point. It is not horizontal. However, the Mean Value Theorem states that somewhere in between a tangent line is parallel to this line. Click on the graph to see a demonstration.